Rhythms

• Talk about the homework.
• Discuss the first presentation and project (due in Week 6)
• Working with rhythms.
• The nPVI metric
• Testing a hypothesis.

Presentation and Paper

Due in Week 6:

• Analyze a large collection of musical works in score format, using Python. Asking some sort of analytical broad question.
• We can provide scores, if you would like, or you can provide your own set of xml scores (we can help with the conversion).
• On the Wednesday of Week 6, you will be presenting your project to the class. The presentation should be no less than 10 minutesm and no more than 15 minutes. Prepare for about 5 minutes of questions.
• Please submit a 5-7 page paper that discusses your project on the Friday of Week 6.

Working with Rhythms

Rhythmic Representation

In Kern Files (Humdrum)

As we've seen, kern files use reciprical notations to show rhythms. Whole notes are notated as "1", half notes as "2", etc.

Tuplets are a bit of a different matter. The handbook states that:

In general, the way to determine the kern equivalent of an arbitrary “tuplet” duration is to multiply the number of tuplets by the total duration which they occupy. If 7 notes of equal duration occupy the duration of a whole-note 1, then each septuplet is represented by the value 7 (i.e. 1 x 7). A more extreme example is 23 notes in the time of a doubly dotted quarter.

So an eighth note triplet, which occupies the space of a quarter note, would be notated with a "12", and quarter-note triplets, which take up two beats, would be notated with a 6.

In Music21

Metric Position

In Humdrum

There are also a number of tools that analyze the metric position of a note, so you can search for instances that happen on the downbeat, for example, or on beats 1 and 3. Humdrum uses a combination of two tools to do this (metpos and timebase).

In music21

In music21, there is a tool called beatstrength which will do it for you. See the example below.

# !pip install --upgrade music21
#!add-apt-repository ppa:mscore-ubuntu/mscore-stable -y
# !apt-get update
!apt-get install musescore
!apt-get install xvfb
import os
os.putenv('DISPLAY', ':99.0')
!start-stop-daemon --start --pidfile /var/run/xvfb.pid --make-pidfile --background --exec /usr/bin/Xvfb -- :99 -screen 0 1024x768x24 -ac +extension GLX +render -noreset
from music21 import *
us = environment.UserSettings()
us['musescoreDirectPNGPath'] = '/usr/bin/mscore'
us['directoryScratch'] = '/tmp'
!sh -e /etc/init.d/x11-common start

littleMelody = converter.parse('tinynotation: 4/4 c4 c4 g g a a g2 f4 f e e d d c2')
littleMelody.show()

for n in littleMelody.flat.notes:
    if n.beatStrength == 1:
      n.show()

###listing all downbeats.
for n in littleMelody.flat.notes:
    if n.beatStrength == 1:
      print(n.nameWithOctave)

Exercise 1: Searching the Polska Collection

Let's try to find out which scale degrees are the most common on downbeats in the Polish folksong collection.

We will first need to talk about getting scale degrees.

humdrum

In Humdrum, this is quite straightforward, as you simply use the deg tool. This requires a key signature already labeled in the piece, though.

music21

It's a bit more complicated in music21, but is also a little bit more flexible.

You first need to run a key-finding algorithm on the excerpt (we will talk about the specifics of key-finding algorithms next week).

Once you have the key, you create a list of pitches, and get the scale degree of each of those in reference to the home key.

###getting the key 
pitch_count = analysis.discrete.KrumhanslKessler(littleMelody)
key = pitch_count.getSolution(littleMelody)
print(key)

### getting all pitches as scale degree.
pitch_count = analysis.discrete.KrumhanslKessler(littleMelody)
key = pitch_count.getSolution(littleMelody)


for n in littleMelody.flat.notes:
  scale_degree = key.getScaleDegreeFromPitch(n.name)
  beat_strength = n.beatStrength
  print(f'{beat_strength}\t{scale_degree}')
  

Back to the exercise.

How can we get all of the scale degrees on downbeats in the entire polska corpus?

###Let's set the google drive up so that we can access those polska files...
from google.colab import drive
import glob
drive.mount('content', force_remount=True)

### your code below...

#### grab all the polska melodies. Perhaps call it file_list.
import glob

def filebrowser(ext="content/MyDrive/python_scratch/polska/*.krn"):
    "Returns files with an extension"
    return[f for f in glob.glob(f'*{ext}')]

file_list = filebrowser()

### your code below
def beat_and_strength(filename):
    
    beat_strength = []
    scale_degree = []

    # open the file so we can read through it

    kern_file = [line.rstrip() for line in open(filename, "r+")]

    # skip file if it has an MX in it, use it if it does not
    # this gets rid of irregular time signatures

    if "MX" not in kern_file:
        melody = converter.parse(filename)
        ### getting all pitches as scale degree.
        pitch_count = analysis.discrete.KrumhanslKessler(melody)
        key = pitch_count.getSolution(melody)
        my_list = []

        for n in melody.flat.notes:
            sd = key.getScaleDegreeFromPitch(n.name)
            if sd is not None:
                scale_degree.append(float(sd))
            else:
                scale_degree.append(0)
            beat_strength.append(float(n.beatStrength))
    else:
        print(filename, "has irregular time signatures. Skipping.")

    # return two arrays
    return [beat_strength, scale_degree]

b_and_s = [ beat_and_strength(filename) for filename in filebrowser()]

print(b_and_s[0])

import matplotlib.pyplot as plt

for i in b_and_s:
    plt.hist(i[0])

for i in b_and_s:
    plt.hist(i[1])

Return and Print

What's the difference between print and return in Python?

So far, our functions have just been printing things out for us to read, but it's important to realize that there is a big difference between print, which shows something for a human to read, and return, which passes the output of one part of code to another.

Using return changes the "control flow" of the program. Using print just shows you something in the console.

### your code below
def beat_and_strength_as_column(filename):
    
    beat_strength = []
    scale_degree = []

    # open the file so we can read through it

    kern_file = [line.rstrip() for line in open(filename, "r+")]

    # skip file if it has an MX in it, use it if it does not
    # this gets rid of irregular time signatures

    if "MX" not in kern_file:
        melody = converter.parse(filename)
        ### getting all pitches as scale degree.
        
        pitch_count = analysis.discrete.KrumhanslKessler(melody)
        key = pitch_count.getSolution(melody)
        my_list = []

        for n in melody.flat.notes:
            sd = key.getScaleDegreeFromPitch(n.name)
            if sd is not None:
                scale_degree.append(float(sd))
            else:
                scale_degree.append(0)
            beat_strength.append(float(n.beatStrength))
    else:
        print(filename, "has irregular time signatures. Skipping.")

    # print an output, but this note that this just a print to the console.
    for beat, scale in zip(beat_strength, scale_degree):
      # return(beat, scale)
      print(f'{beat}\t{scale}')

for file in file_list:
  beat_and_strength_as_column(file)

Counting All Downbeats

Here's a solution (adapted from Dr. Tan's code) that counts all of the downbeats, and then graphs the scale degree.

downbeat_scale_degrees = []
for file in file_list:
  piece = converter.parse(file)
  for n in piece.flat.notes:
    ## added these two lines to the loop.
    pitch_count = analysis.discrete.KrumhanslKessler(piece)
    key = pitch_count.getSolution(piece)
    scale_degree = key.getScaleDegreeFromPitch(n.name)
    beat_strength = n.beatStrength
    if beat_strength == 1:
      downbeat_scale_degrees.append(scale_degree)

db = [] 
for sd in downbeat_scale_degrees: 
    if sd != None : 
        db.append(sd) 

values, counts = np.unique(db, return_counts=True)
print(f'{values}\n{counts}')

import matplotlib.pyplot as plt
plt.hist(db)

Testing a Hypothesis

H1: Are pieces in the Polish folksong corpus more "rhythmically complex" than another corpus? "Complex" is obviously a pretty loaded term, and it isn't really not something that can be formalized, but "variability" might be thought of as a proxy for complexity.

The normalized variability index (nPVI) has been used extensively over the past few years as a way of examining rhythmic variability in melodies. It's adapted from linguistics (Grabe and Low, 2003) looking at the rhythmic variability of speech. Patel and Daniele (2004) argued that the variability of melodies can be correlated with the composer's native language.

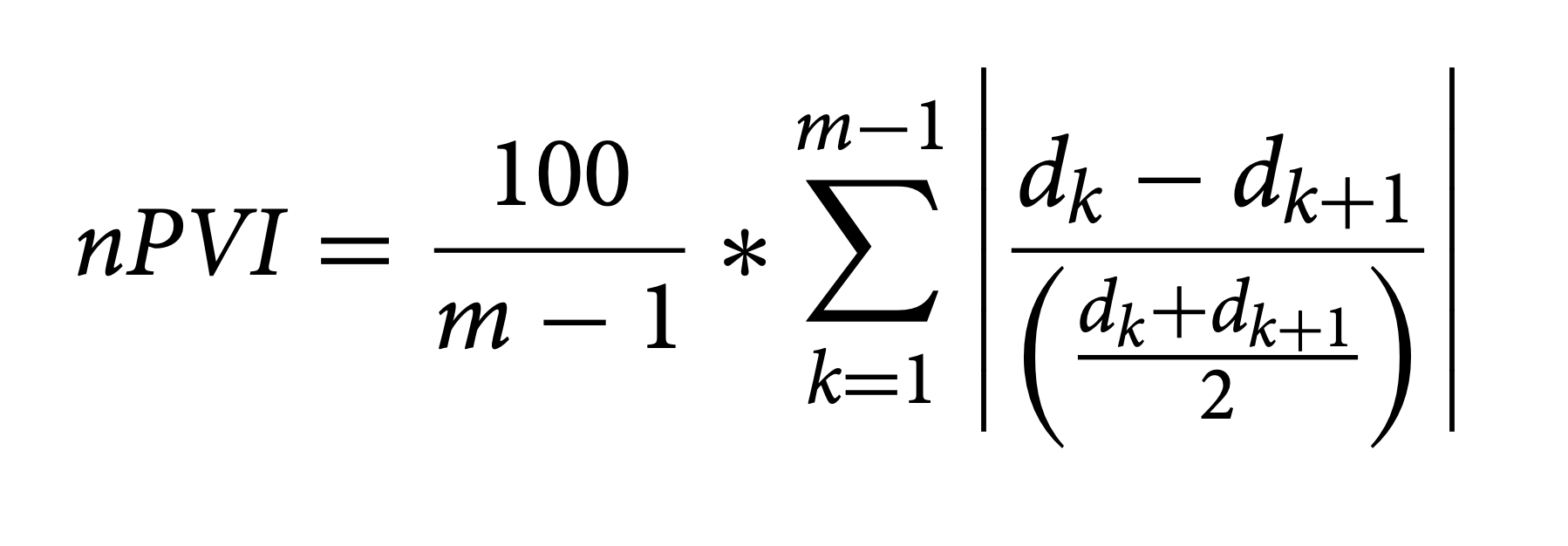
Let's break down how we might break this down into a function we could implement.

Getting Rhythmic Content

For the nPVI tool, we will need to strip all non-rhythmic data. This means getting rid of all metadata, pitch content, and barlines. Kern files look at rhythms reciprocally, in that a whole-note is a 1, and eighth-note is an 8, etc. We will first need to arrange those durations so that a lower number equals a shorter rhythm.

Here's a brief reciprocal rhythm function for that. Let's break this function down a bit.

def recip_rhythm(tune):
  
  melody = [line.rstrip() for line in open(tune, "r+")]
	## define some empty lists that we might need later.
  x = []
  y = []

  ## for every line in the melody, if there is no !, =, or *, print the line.
  ## this gets rid of metadata and barlines. It puts everything into the
  ## x list.

  for f in melody:
    if "!" not in f and "=" not in f and "*" not in f:
      x.append(re.sub("[^0-9._\]\[]", "", f))

  for i in x:
    if "." not in i:
      i = float(i)
      recip = 1/i
      y.append(recip)

    else:
      no_dot = re.sub("\.", "", i)
      no_dot = float(no_dot)
      recip = (1/no_dot)+((1/no_dot)*.5)
      y.append(recip)

  return(y) 

def npvi(tune):
  rhythm = recip_rhythm(tune)
  mel_length = 100/(len(rhythm) - 1)
  total = [abs(rhythm[onset] - (rhythm[onset+1])/(rhythm[onset] + (rhythm[onset+1]/2))) for onset in range(len(rhythm)-1)] 
  total_sum = sum(total)
  answer = (mel_length * total_sum)
  return([tune, answer])

The above loop that begins with "for i in x" focuses on dotted rhythms. It goes through that x list, and If there is no dot, then just turn i into a float, and put it in the list. The equation under the recip function basically says: if you find a dot, that means it's the rhythm plus half of that rhythm.

The nPVI equation.

Now that we have the data in this format, we can just run the nPVI equation on the melody. This is the nPVI equation, when fed the list from the recip_rhythm function. See Daniele and Patel (2004) for full explanation of it.

The nPVI rating is sum of the the distance between two successive onsets (dk-dk+1) divided by half of the sum of those. The absolute value fo this is multiplied by 100 over the degrees of freedom (the number of notes in the melody minus 1).

###Let's set the google drive up so that we can access those polska files...
from google.colab import drive
import glob
import re
drive.mount('content', force_remount=True)

def polish(ext="content/MyDrive/python_scratch/polska/*.krn"):
    "Returns files with an extension"
    return[f for f in glob.glob(f'*{ext}')]



def czech(ext="content/MyDrive/python_scratch/czech/*.krn"):
    "Returns files with an extension"
    return[f for f in glob.glob(f'*{ext}')]

polish_melodies = polish()
czech_melodies = czech()

pnpvi = []
cnpvi = []

for file in polish_melodies:
  x = npvi(file)
  pnpvi.append(x)

for file in czech_melodies:
  y = npvi(file)
  cnpvi.append(y)

print(cnpvi)

from scipy.stats import ttest_ind
t_test = ttest_ind(pnpvi, cnpvi)
p_value = t_test[1]
t_stat = t_test[0]

if p_value > .05:
  print(f'"Ack! This isn\'t significant." The p-value is {p_value}, and the t-statistic is {t_stat}')
elif p_value < .05:
  print(f'"Hooooooooray!!!" I can publish this weird little study. The p-value is {p_value}, and the t-statistic is {t_stat}')