A Brief History of Key-Finding¶
Key-finding has historically been closely tied with the computationalist approach to cognition. Modeling how a computer might infer the key of a piece can be an interesting problem that allows us to ask how we might be inferring keys.
For that reason, the correct answers are interesting, but not as interesting as the process and (sometimes) the mistakes.
Longuet-Higgins¶
One of the first key-finding algorithms was Longeut-Higgins' shape-matching algorithm (1976), which would use the process of elimination over the course of a piece. For example, if the first note was "C", D-major, A-major, E-major, F#-major, B-major, G-flat major, etc were all eliminated. If the next note was an B-natural, the choices were limited even further.
This method worked quite well with very tonal monophonic pieces, and surprisingly it was able to get all of the keys for Bach's Well-Tempered Clavier.
Overall, howver, it struggled with pieces that included functional chromaticism, and polyphony, in general.
Krumhansl-Schmuckler/Krumansl-Kessler¶
THe Krumhansl-Schmuckler model (1990) used a more experimental approach. It took the probe-tone ratings from an earlier experiment (Krumhansl and Kessler, 1982) to find the most likely tones in a piece.
In these probe tone experiments, participants would be presented with a cadence, followed by a tone. They would then rate the "goodness-of-fit" of each of these tones. This would generate a key-profile, that looked like this:
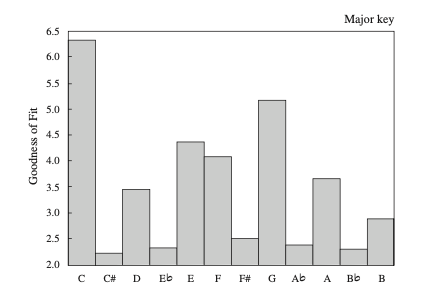
The key-finding algorithm would take the pitch count of each piece, and then run a correlation with this profile for each key. So if the total number of pitches against this key-profile provided a correlation of .80, and the others provided a correlation of .76, .74, etc. the highest number would be taken as the correct key. We might call this a correlational approach to key-finding.
The algorithms below use this approach, as well, but whereas this model uses the ratings from an experiment, the others use specific corpora.
Aarden-Essen¶
Bret Aarden (2003), for example, collected the pitch count of the entire Essen Folksong Collection (Schaffrath, 1995). His argument was that the "relationship between 'key-profile' and musical structure' is not as straightforwad as is often assumed." Real musical data, he argued, is more in line with what people have been exposed to.
Bellman-Budge¶
Bellman (2005) used a corpus curated by Helen Budge's stydy if chord frequencies of 18th and 19th century composers.(1943) It's a correlational model, but with Western Art Music.
Temperley-Kostka/Payne¶
Temperley (2001) curated the Kostka-Payne corpus, which included all of the musical examples from the Kostka-Payne textbook.
Craig Sapp's Simple Weightings¶
Sapp (2011) proposed a simple set of scale degree weights to be used with the Krumhansl-Schmuckler algorithm, con- sisting of only 2 (for tonic and dominant, 1 (for other diatonic tones), and 0 (for non-diatonic tones).
Despite the fact that it is technically using "less information", the algorithm outperfoms the Krumhansl-Schmuckler algorithm, and many others.
Results¶
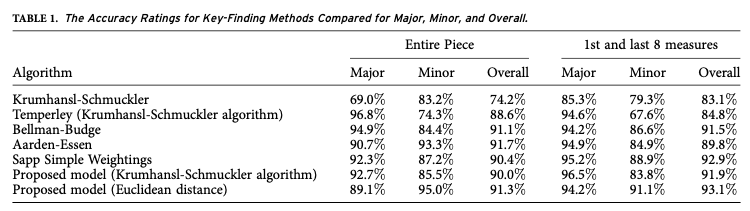
Here is a table of results (from Albrecht and Shanahan, 2013):